第八讲 外部性和公共品 MWG 11.A-11.C

福利经济学定理与市场失灵

• 福利经济学第一定理：竞争均衡一定是帕累托有效的
• 前提条件
• 前提不成⽴：噪⾳、污染，等等
• 两类市场失灵（market failures）：外部性（externalities）、公共品（public goods）

外部性

• 定义：消费者的福利⽔平（效用）或⽣产者的⽣产技术受到市场上其他主体⾏为的“直接”影响
• “直接”：不包括通过价格的间接影响（货币外部性，pecuniary externality）
• 负的外部性：⽅便⾃⼰，损害他⼈
• 正的外部性：⾟苦我⼀个，幸福千万家

刻画外部性的模型

• 局部均衡模型中的两个消费者，价格和收⼊不受⾏为影响（两人只占经济的很小一部分）

• 拟线性效⽤函数

• 始终消费者1产生负外部性，消费者1的⾏为直接影响⾃⼰和消费者2的效⽤

• 给定⾏为，先最优化消费，然后决定最优⾏为

  $$u_i=g_i(x_i,h)+m_i,\ i=1,2$$

  直接影响体现为 $h$ 直接进入效用函数，预算约束（等式）为

  $$px_i+m_i=w_i$$

  于是效用函数可化为

  $$u_i=g_i(x_i,h)-px_i+w_i$$

  对于消费者1

  $$u_1=g_1(x_1,h)-px_1+w_1 \\ \partial u_1/\partial x_1=\partial g_1/\partial x_1-p=0,x_1^*=x_1(h,p) \\ u_1=g_1(x_1(h,p),h)-px_1(h,p)+w_1=\phi_1(h)+w_1$$

  一般地

  $$u_i=\phi_i(h)+w_i$$

市场均衡与帕累托有效中的最优⾏为

• 市场均衡与帕累托有效的⼀阶条件

  • 帕累托有效

    $$\max\limits_{h} \phi_1(h)+\phi_2(h)+w_1+w_2,\phi_1'(h^o)+\phi_2'(h^o)=0$$

  • 市场均衡

    $$\max\limits_{h} \phi_1(h)+w_1, \phi_1'(h^*)=0$$

  • 假设 $\phi_1'(h)>0,\phi_1''(h)<0$¹

  • 假设负外部性 $\phi_2'(h)<0$，正外部性 $\phi_2'(h)>0$，而且 $\phi_2''(h)<0$，即负外部性时意味着加速下降，正外部性意味着边际递减

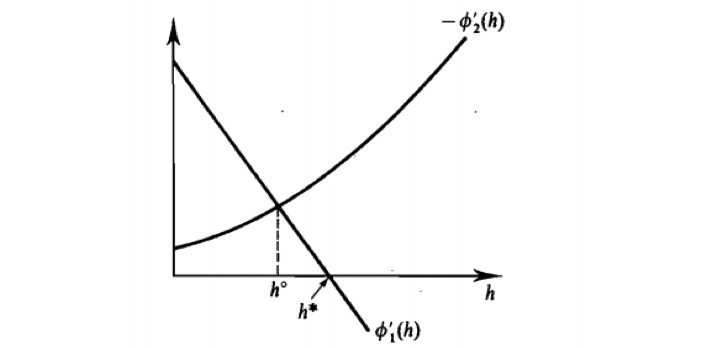
• 外部性为负时：数学推导和⼏何关系（此时 $-\phi_2'(h)$ 在横轴上方）

  • $h^*>h^o$：反证法，假设 $h^*\leq h^o$，则 $0=\phi_1'(h^*)\ge \phi_1'(h^o)$，则 $\phi_2'(h^o) = -\phi_1'(h^o) \ge 0$，与负外部性矛盾

• 外部性为正时：数学推导和⼏何关系（此时 $-\phi_2'(h)$ 在横轴下方）

  • $h^*<h^o$：反证法，假设 $h^*\ge h^o$，则 $0=\phi_1'(h^*)\leq \phi_1'(h^o)$，则 $\phi_2'(h^o) = -\phi_1'(h^o) \leq 0$，与正外部性矛盾

• 个⼈总是倾向于产⽣过多的负外部性或者过少的正外部性

解决外部性的传统⽅法

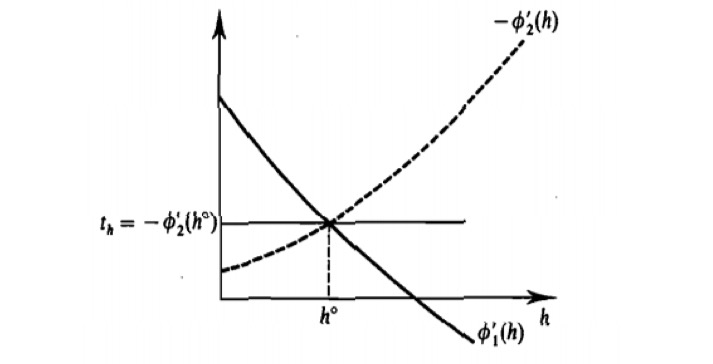
• 配额（Quota）：直接向产⽣外部性的⾏为征收

• 庇古税（Pigouvian taxation）

  $$\max \phi_1(h)+w_1-th \\ \phi_1'(h)-t=0 \\ t=\phi_1'(h^o)=-\phi_2'(h^o)$$

• 配额和庇古税率的确定要求政府对消费者偏好有完全信息

市场主体协商解决

• 始终是消费者1放噪音

• 当消费者2说了算时：take-it-or-leave-it offer，$(h,T)$

  在消费者1接受的情况下消费者2最大化自己的效用，消费者1接受的条件：

  $$\phi_1(0)+w_1 \leq \phi_1(h)+w_1-T$$

  给定$h$，消费者2总会增大 $T$ 直到

  $$\phi_1(0)+w_1 = \phi_1(h)+w_1-T \\ T=\phi_1(h)-\phi_1(0)$$

  消费者2的最优化

  $$\max\limits_{h} \phi_2(h)+w_2+T=\phi_2(h)+w_2+\phi_1(h)-\phi_1(0)$$

  解恰为社会最优

  $$\phi_1'(h^o)+\phi_2'(h^o)=0$$

  最终的offer为 $(h^o,\phi_1(h^o)-\phi_1(0))$

• 当消费者1说了算时

  初始噪音 $h^*$，offer为消费者2用 $T$ 换取消费者1减少噪音 $h$，对于消费者2

  $$\phi_2(h^*)+w_2 \leq \phi_2(h^*-h)+w_2-T \\ \phi_2(h^*)+w_2 = \phi_2(h^*-h)+w_2-T \\ T=\phi_2(h^*-h)-\phi_2(h^*)$$

  消费者1的最优化

  $$\max_h \phi_1(h^*-h)+w_1+\phi_2(h^*-h)-\phi_2(h^*) \\ -\phi_1'(h^*-h)-\phi_2'(h^*-h)=0$$

  于是 $h^*-h=h^o$，仍为社会最优

• 科斯定理（Coase theorem）

  • 外部性（externality）被内部化（internalize），将外部性重新纳入市场
  • 表述：在产权明晰、交易成本为零的条件下，无论初始产权如何配置，个体自发地对外部性进行协商，总能达到社会最优
  • ⽐配额和庇古税的优势：不需要政府对消费者偏好有完全信息
  • 注意：信息（需要的信息更少）、交易成本（协商可能产生费用）、效⽤函数（拟线性效用等）、制度环境（自发协商）

公共品

• 定义：如果⼀个市场主体对某种商品的使⽤并不排除其他市场主体对它的使⽤，那么这种商品就是公共品
• ⾮排他性（根本标准），如知识
• 公共品不⼀定是“好”的（public bads），如污染的空气

社会最优公共品数量

• 只关注公共品的局部市场

• 公共品 $x$ 带来的效⽤

  $$u_i=\phi_i(x)+m_i, i=1,2,\cdots,I$$

• 公共品 $x$ 的⽣产成本

  $$c(x),c'>0,c''>0$$

• 社会最优数量

  $$\max\limits_x \sum\limits_i \phi_i(x)+ \sum\limits_i m_i-c(x) \\ \sum\limits_{i} \phi_i'(x)=c'(x)$$

  公共物品最优数量的条件：在公共物品的最优水平上，消费者在该公共物品身上得到的边际效用之和，等于它的边际成本

如果公共品由私⼈购买

• 消费者问题

  $$\max\limits_{x_i} \phi_i(x_i+\sum\limits_{j \neq i}x_j^*)+w_i-px_i \\ \phi_i'(x_i^*+\sum\limits_{j \neq i}x_j^*)=p \\ \phi_i'(x^*)=c'(x^*)$$

• ⽣产者问题

  $$\max_p px-c(x),p=c'(x)$$

• 市场均衡条件 $\rightarrow$ 公共品提供不⾜

  反证法：假设 $x^* \ge x^o$，社会最优

  $$\sum\limits_{i} \phi_i'(x^o)=c'(x^o)$$

  私人购买

  $$\phi_i'(x^*)=c'(x^*)$$

  假设 $x^* \ge x^o$，则

  $$c'(x^*) =\phi_i'(x^*) \leq \phi_i'(x^o) < \sum\limits_{i} \phi_i'(x^o)=c'(x^o)$$

  成本函数 $c''>0$，则 $c'(x^*)\ge c'(x^o)$，矛盾

• 角点解：搭便⻋现象（free-rider problem）

  $$\phi_i'(x^*)<c'(x^*)=p,x^*=0$$

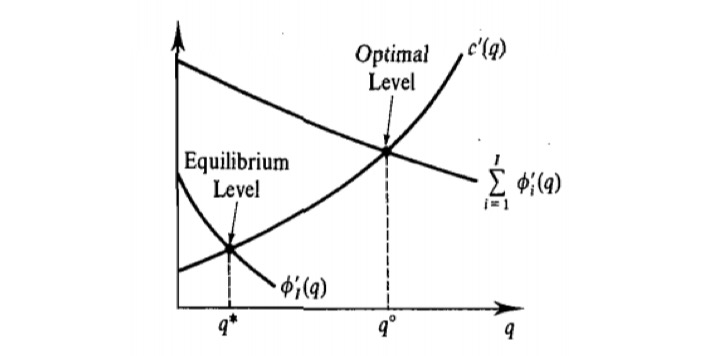
  不失一般性，均衡时

  $$\phi_1'(x)<\phi_2'(x)<\phi_3'(x)<\cdots<\phi_I'(x)=p$$

  意味着提供公共物品的消费者只有唯一一个，即能从公共物品身上得到边际效用最大的那个消费者

• ⼏何图示

解决公共品提供不⾜的⽅法

• 政府提供

• 补贴机制：以多⼈为例

  消费者：

  $$u_i=\phi_i(x_i+\sum_{j \neq i}x_j^*)+w_i-px_i+t_i x_i \\ \phi_i'(x^*)=p-t_i$$

  生产者：

  $$p=c'(x)$$

  均衡：

  $$\phi_i'(x^*)=c'(x)-t_i \\ \phi_i'(x^o)=c'(x^o)-t_i=\sum\limits_{i} \phi_i'(x^o)-t_i \\ t_i=\sum\limits_{j\neq i}\phi_j'(x^o)$$

• 私⼈购买公共品的使⽤权：Lindahl均衡

  消费者：

  $$u_i=\phi_i(x_i)+w_i-p_ix_i,\phi_i'(x_i)=p_i$$

  生产者：

  $$\sum\limits_{i} p_i x-c(x)=0,\sum\limits_{i}p_i=c'(x)$$

  均衡：

  $$\sum \phi_i'(x)=\sum p_i=c'(x)$$

  社会最优：

  $$\sum \phi_i'(x^o)=\sum p_i=c'(x^o)$$

• 林达尔均衡不见得有可操作性

  • 必须能够阻止消费者使用公共品，否则消费者没有理由相信不购买就无法消费公共品
  • 每个市场只有一个消费者，价格接受者假设不合理
  • 难以自发显示个人偏好，消费者有激励低报自己的偏好，期望别人会支付

勤奋的学⽣

例（参见MWG课后习题11.D.1-B）：班上有 $I$ 个⼀样的学⽣，学⽣ $i$ 的学习时间是 $h_i$，相应的效⽤损失是 $h_i^2 /2$。学⽣ $i$ 的效⽤取决于他相对于其他同学的努⼒程度 $\phi(h_i /h)$，其中 $h$ 是全体学⽣的平均学习时间。假设各同学的均衡学习时间是⼀样的，求该均衡学习时间，并与帕累托最优的学习时间⽐较。

学生 $i$ 的效用最大化

其中，$h=\sum h_i/I$，则一阶条件为

由于同学的均衡学习时间相同，即 $h_i=h$，则

社会最优，均衡学习时间相同时

等价于

于是 $h^o=h_i^o=0$

每个学生施加负外部性，竞争的结果是学习过度

公地悲剧

例（参见MWG课后习题11.D.5-B）：渔民可以去湖上打渔。每次出船的成本是 $r > 0$。如果湖上有 $b$ 艘船，那么总捕鱼量为 $f(b)$，也即⼈均捕⻥鱼量为 $f(b)/b$，且$f’(b) > 0, f’’(b) < 0, f(0) = 0$。鱼的售价是 $p > 0$，不受捕鱼活动的影响。

1. 均衡条件下，湖上有多少艘船在捕鱼？
2. 社会最优的捕鱼船的数量是多少？与 1 的结果⽐较。
3. 如果对每艘船征收打渔税，最优税率应是多少？
4. 如果湖由个⼈所有，那个⼈决定最优的渔船数量。最优的数量应该是多少？

1. 均衡时，对于最后一个决策的渔民来说，出船的边际收益等于边际成本

2. 社会最优

3. 征税

4. 个人所有的问题与社会最优相同